Part II: Euclid’s Poetic
1. The Tragic Narrative
revised 8August 2010
In an earlier posting, I drew attention to Euclid’s rhetoric, ending with a promise to follow this with a post on his poetic. This entry is meant to fulfill that promise – but first, it will be essential to explain the sense in which the term poetic is being used. I follow Aristotle, who in his Poetics has drama primarily n view, so we’ll be reading the Elements as high drama.
The soul of the drama, Aristotle believes, is the MYTHOS, the story, and indeed, Euclid is telling a remarkable tale. It is a trilogy, in the pattern of Aeschylus’ Oresteia, in which we pass from a path of early triumph to the darkness of despair – and only finally, in the third play, discover a way forward of a brilliantly new sort.
In the first play, Agamemnon, returning triumphant from the Trojan war, is murdered by his queen Clytemnestra. Next, in the dark logic of timeless vengeance, she must in turn be murdered by her own son, Orestes. This most heinous of crimes leaves Orestes in terrifying darkness, the hands of the avenging Furies, against whose iron grip enlightened reason appears to hold no power. Only in Athens, the city of Athena, will rescue become possible from this endless logic of retribution. Finally, in the third play, at the point of crisis, the Furies are perceived to waiver. At a word from Athena, they turn: time holds its breath, and through the subtle wit and rich wisdom of the goddess, they prove at last, persuadable. They catch some dawning image of hope, of purpose, of a good beyond the blind, literal logic of their law. From agents of death they might become nurses of life, to be celebrated as agents of abundant harvests. With this opening, a new Athenian law-court is founded, in which reason directed to the good triumphs over the Furies’ old law of consequence and necessity. Performance of Aeschylus’ play was to become a civic ritual, in which the assembled city would be reminded, through the experience f terror and its release, the foundation in a higher, human reason, of the Athenian polis.
Can we imagine that Euclid’s drama reaches to such extremes of darkness and of light? Almost startlingly, we find that it does. This is not, indeed, the customary way in which a work of mathematics is to be read. Nor is it usual to find a relationship, at this deepest level, among the political, the mathematical, and the poetic. Yet this, I propose, is the reach of Euclid’s poetic.
2. Tragic Crisis in the Elements
At the heart of Greek mathematics lies the problem of continuity, for which Aristotle uses the word SYNECHEIA, “holding together’. The Pythagorean Theorem – whose traditional name already suggests its mystic portent –makes its appearance as Euclid’s Proposition I.47, at the culmination of the first book of the Elements. There, it marks as well the beginning of a reign of innocence which will last through the first four books: we build a succession of figures and explore their relationships with no apparent reason to doubt that our foundation is secure. Silently but inexorably, however, this innocent theorem will be leading us into confrontation, at the close of Book IV, with a mystery hidden in the hypotenuse of that equilateral right triangle – the diagonal, that is, of a square. No longer the simple line it had appeared, it will be revealed as a yawning chasm, seat of the darkest of mysteries – the mystery of the continuum. Since any straight line can become the diagonal of such a square, every straight line must harbor the same abyss.
The proposition itself demonstrates as we all know, that in a right triangle, the sum of the squares on the sides equals the square on the hypotenuse. We learn this today as school children, and take it as familiar knowledge thereafter, but it brought Greek thought to a standstill, plunging mind into the darkness of mystery: the very cave of the Furies. How could that be?
The answer lies in the proposition to which this one leads – one however which Euclid takes care to bury in silence, and leave unspoken. It lies too close to the heart of mystery.
It is easy to prove, on the basis of the Pythagorean Theorem, that “If a number measures the side of a right triangle, no number exists which will measure the diagonal. To appreciate its force, we have to pause to ask, “What is number?” To which the answer is: Every number is a multiple of the unit. Thus if we write for example 1.414, we refer to a number which is 1,414 “thousandths”, or the 1,414th multiple of .001, chosen as unit. Every number is in this way some multiple of some unit.
Very well: by means of number in this way the rational mind, LOGOS, can know, and precisely name, every length – can it not? In the darkness of Euclid’s unspoken proposition, the answer is “No!”. The diagonal of the right triangle clearly has a length: we have just made that clear in the Pythagorean Theorem itself. But the secret proposition (imparted orally, we may be sure, to chosen students) makes it clear as well that LOGOS cannot know this length. If LOGOS cannot know this simplest of all entities, there must be no bounds to what mind cannot know.
Aristotle takes up this problem of the continuity of the straight line in his Physics, as foundational to the integrity of the cosmos itself, in all its aspects and all its levels. If the straight line fails, all else fails with it...
Here is the problem. Suppose we attempt to fill the line with all the thinkable multiples, however large, of all the thinkable units, however small. We can generate an infinity of points, corresponding to the rational numbers – yet the unspoken theorem implies immediately that we will have missed at least as many points as we filled. Indeed, our rational points actually leave the line infinitely more empty than it is full, and thus devoid of any semblance of intelligibility. We know that the diagonal of the square exists; but we know as well, by its dark corollary, that we cannot know its length, or the lengths of an infinity of infinites of other lengths within its length. LOGOS is at once the mental faculty by which we speak (and in that sense, the word means the spoken sentence – in turn, Latin for “thought”), and ratio or number, as a measured length is known by its ratio to the unit. Not being able to measure, means that mind, as LOGOS, has been struck dumb.
This is, then, the moment of darkness for LOGOS, the confrontation with the irrational, the ALOGOS. Plato sees this in the Dialogues as the threatening darkness of the entrance to ELEUSIS, the site of the mysteries, as well as the APORIA, the impassible sticking-point, in the dialectical argument itself. As Euclid and Plato both know well, it is figured in the despair of that tragic hero at the crisis of the trilogy. Literal LOGOS, counting sins and reckoning consequences in the manner of the Furies, leads the mind only to emptiness and distraction. If Euclid were to leave his project at this point, it would lie in ruins. In tragedy, this is the terrifying cave of the Furies, with whom it is impossible to reason in any higher sense. For Aeschylus, as we have seen, at this point of crisis, Athena intervenes with just such a new form of reason, a reason which looks beyond the reckoning, of LOGOS, to a vision of the beautiful and the good. What hint will Athena now whisper, in Euclid’s ear?
For Euclid, the hold of LOGOS is broken by the introduction of something new, which he calls magnitude: a way of measuring beyond the counting-logic of number; a way by which mind can embrace the wholeness of the line. For Plato in the Republic, it is the passage from the cave of LOGOS to the light of NOUS. The word mystery derives from the verb MUEIN, to be silent. NOUS is silent knowing, direct, wordless intellectual insight of a truth beyond words. This is the art of Athena, which awakened a saving hint of recognition in the wits of the Furies, and made the Athenian law-court, and with it the Athenian polis, possible. What word will Athena now whisper in Euclid’s ear, to save his Elements – and with them, it would seem, the wholeness of the intelligible cosmos?
3. ELEUSIS
Euclid’s plot has moved forward at a vigorous pace, offering to mind an unfolding sequence of intuitive objects. Now, in Euclid’s strange Book V, time stops, and the intuitive mind will be given no object on which to settle. There will be no countable or measurable objects: we will be making our way out of the realm of counting- number, which has betrayed us. Instead, we are to speak in words which have no objects: in terms of something Euclid calls magnitude (MEGETHOS) – the word Athena must have whispered n his ear! Today we call these irrational numbers, but as we see, for the Greek mind this is simply a contradiction in terms (ALOGOS LOGOS – the illogical logical!). It is a new and different abstract realm, in which mind enters upon a quest of its own. For Euclid, this quest is decisive: our goal is to restore mind’s relation to those real and most beautiful mathematical objects, which at the end of Book IV seemed to have been rendered utterly inaccessible.
The role of Book V, then, will be to open to mind a path which seemed to have been denied it: a path, beyond LOGOS, to the direct intuition of those most beautiful figures, the regular geometrical solids with which the Elements will close.
We cannot follow here the intricacies by which Euclid achieves this in Book V; even the definition of same ratio, with which the book begins, is daunting. We can say, however, however, that in Book V he accomplishes to perfection the limiting process we know today as Dedekind’s cut, Dedekind carries out in analytic terms essentially what Euclid had done two thousand years before. By carrying the measuring process to an infinite limit, it restores the power of mind to address all things – not however, as LOGOS, but after this mystic passage, as that intellectual intuition termed NOUS. We began with NOUS in the first books, but lost trust in it with what seemed the catastrophe of reason at the close of Book IV. Now, by way of the abstract concept of MEGETHOS – length, in a sense, without object – NOUS is once again accredited, and the way is open to our intellectual delight in the procession, in Book XIII, of the regular solids.
4. NOUS the Way of Intuitive Mind
There is a telling analogy here: Aethena in Aeschylus’ third play makes very certain that Athens will remember and celebrate the Furies, who have hitherto been so terrifying. Indeed, the tragedy is just that civic remembrance, and celebration. The Athenian mind, purified by the experience of tragedy, has been strengthened to the point of carrying the polity through situations which will continue to be suffused with the irrational.
Surely it is in the same spirit that Euclid makes certain to track the irrational as it appears at every turn, appearing everywhere the construction of the regular figures. To track it, he must first name it: endow the ALOGOS with LOGOS!
The powers of Book V enable him to do just that, by way of a newly empowered intuitive mind. NOUS contemplates the regular solids now in the full measure of their regularity and symmetry, but at the same time with hard-won awareness of their infusion with the darkness of the barely-speakable. They are no less beautiful – indeed, perhaps more wondrous – for being tragic figures.
5. The Dodecahedron: Noetic Being
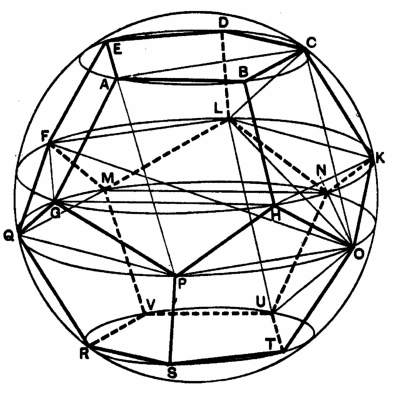
The dodecahedron (regular solid of twelve faces) is the cumulating figure in Euclid’s sequence of construction of the regular solids. (Proposition 17 of Book XIII). Euclid is careful to include, in the case of each solid, that if the radius of the enclosing sphere is rational, then each s of the equal edges will be an irrational line. And in each case, by way of the powers of Book V, the irrational has been specified and given what we might well think of as a mystic name. It has been the work of Book X, ascribed to Theaetetus, to work through this daunting project, and construct, in effect, a dictionary of the irrational.
Here in Euclid’s final figure, mind comes to rest on such a weave of the rational and the irrational. Here, if the radius of the enclosing sphere is rational (taken as our unit of measure) then every edge of the dodecahedron will be the irrational known as APOTOME. The name has been hard-won, as each of these rational-irrationals has been systematically constructed and blessed with its mystic name in the course of Book X. The APOTOME was christened in Prop.73 of that book.
We would be entering a very different mathematical world if we were to translate the APOTOME’s construction into the language of Descartes and modern algebra. But it may be of interest, and suggestive of the complexity of the heroic labors of Theaeteus, to know that the analytic formula for the edge of the dodecahedron looks like this:

Here, r is the radius of the inscribed sphere, and the rational unit in this case.
(Heath’s Euclid, III, p. 510)
6. A Closing Note
Recalling our initial claim, concerning Euclid’s rhetoric, we see that he has despite all odds remained true to his original plan. He appeals in the construction of this last figure, as he did in his first, that equilateral triangle, to the reader’s agreement by way of intellectual intuition, NOUS, rather than to any binding chain of LOGOS. That insight has become, under Euclid’s guidance, stronger, deeper and wiser than it was when it first looked upon the equilateral triangle. We could not have imagined then, as we now know, the overwhelming probability that the lines of the first triangle, if chosen by chance, would be unmeasurable, and inaccessible to LOGOS. Euclid’s Elements thus stand with the wisdom of Aeschylus, as witness to the power of intuitive mind.
We know well that our contemporary world has not followed that heroic path. There is more than one path to take out of the depths of ELEUSIS, whose abstract magnitude threatens to dissolve all substance. Euclid rescues substance; Descartes, embracing the abstraction of MEGETHOS, which he translates as extension, turns the world into one universal algebra, one universal “x”.
Book V thus stands at a crossroads of history, the point at which our contemporary culture left all ancient constraints behind. But that is by no means the only train of thought open to us in the modern world; Euclid’s wisdom survives today in other forms.
To explore more fully the depths of Book V and its implications for our position today would surely be work for a further blog posting. Meanwhile, as ever, comments on this one are earnestly invited.












